简单数学:已知三角形三边,求三角形面积
终于我们来到最后一个部分,今天我们要用三角形的三条边求出三角形的面积
前提
我大致推导了一下,大概需要以下几个前提,我们才能根据三边长来求出面积:
- 三角形的面积:$S = {ah \over 2}$
- 相似直角三角形,直角边成比例:${a_1 \over h_1} = {a_2 \over h_2}$
- 勾股定理(畢氏定理):$a^2 + b^2 = c^2$
本文是最后一部分。
已知条件
我们在 c 边做一条高 h,这条高把 c 边分为两段 $c_1$ 和 $c_2$:
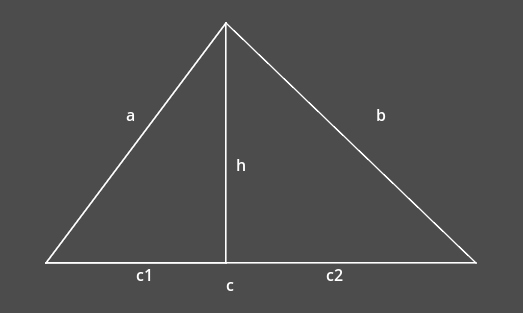
所以我们可以知道,只要求出 h,我们就可以计算出三角形面积,根据勾股定理,我们可以有:
$$ \begin{cases} \begin{alignat}{7} &c_1+&c_2 &=c \kern{3em}\newline &c_1^2+&h^2 &=a^2 \kern{3em}\newline &c_2^2+&h^2 &=b^2 \kern{3em}\newline \end{alignat} \end{cases} $$
三个方程,三个未知数,利用一些变换,求解也不会很难,$(2)-(3)$可以得到:
$$ \begin{alignat}{2} c_1^2 - c_2^2 &= a^2 - b^2\newline (c_1 - c_2)(c_1 + c_2) &= a^2 - b^2\newline c_1 - c_2 &= {a^2 - b^2 \over c} \end{alignat} $$
$(6)+(1)$ 可以得出:
$$ \begin{alignat}{2} 2c_1 &= {c^2+a^2-b^2 \over c} \newline c_1 &= {c^2+a^2-b^2 \over 2c} \end{alignat} $$
我们把 $c_1$ 代入 $(2)$:
$$ \begin{alignat}{3} h^2 &= (a-c_1)(a+c_1) \newline &={ (2ac -c^2-a^2+b^2)(2ac+c^2+a^2-b^2) \over 2c \cdot 2c} \newline &= { [b^2 -(a-c)^2][(a+c)^2-b^2] \over 4c^2} \newline &= { (a+b-c)(b-a+c)(a+b+c)(a+b-c)\over 4c^2} \newline \end{alignat} $$
所以我们就可以算出 $h$ :
$$ h = {\sqrt{\smash[b]{(a+b+c)(a+b-c)(b-a+c)(a-b+c)}} \over 2c} $$
那么三角形的面积就是:
$$ S = {ch \over 2} = {\sqrt{\smash[b]{(a+b+c)(a+b-c)(b-a+c)(a-b+c)}} \over 4} $$
总结
如果我们定义$s$ 为三角形周长的一半:
$$ s = {a+b+c \over 2} $$
那么面积公式可以进一步化简:
$$ \begin{alignat}{3} S&= {\sqrt{\smash[b]{(a+b+c)(a+b-c)(b-a+c)(a-b+c)}} \over 4} \newline &= {\sqrt{\smash[b]{(a+b+c)(b-a+c)(a-b+c)(a+b-c)}} \over 4} \newline &= {\sqrt{\smash[b]{{a+b+c \over 2} \cdot ({a+b+c\over 2} - a)\cdot ({a+b+c\over 2} - b)\cdot ({a+b+c\over 2} - c)}}} \newline &= {\sqrt{\smash[b]{s(s-a)(s-b)(s-c)}}} \end{alignat} $$
如果你还有印象的话,这个就是海伦公式了,好了我们的目标达成了, 能够看到这里的读者,希望你也能感受到数学的魅力。